In geometry, we often deal with simple shapes — squares, rectangles, triangles — and calculating their areas is typically straightforward. But what if you encounter a rectangle-like shape that isn’t perfect — say, the corners aren’t right angles, or the sides aren’t all straight or equal? This is when the concept of an irregular rectangle comes into play.
While breaking the shape into rectangles is a common strategy, Heron’s Formula provides a powerful method when you’re working with triangular sections — especially when dealing with non-right angles or slanted sides. Let’s explore how.
What is Heron’s Formula?
Heron’s Formula is used to calculate the area of a triangle when the lengths of all three sides are known.
The Formula:
If a triangle has sides of length a, b, and c, then:
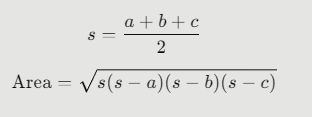
Where:
- sss is the semi-perimeter of the triangle.
- The square root expression gives the triangle’s area.
Why Use Heron’s Formula for Irregular Rectangles?
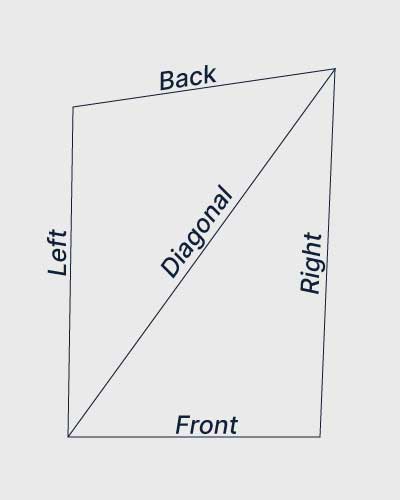
An irregular rectangle can sometimes be split into two triangles by drawing a diagonal between two opposite corners. If the shape is not perfectly rectangular, the diagonal divides it into two non-right triangles.
Using Heron’s Formula allows you to calculate the area of each triangle separately, then add them together to find the total area of the shape.
Step-by-Step Guide: Using Heron’s Formula for an Irregular Rectangle
Step 1: Divide the Irregular Rectangle
Draw a diagonal line from one corner to the opposite corner. This will create two triangles.
Step 2: Measure the Sides of Each Triangle
Label each triangle’s sides (a, b, c). You can measure these using a ruler, scale, or CAD software depending on your application.
Step 3: Apply Heron’s Formula
For each triangle:
- Calculate the semi-perimeter:
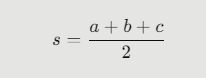
2. Use the formula:
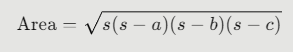
Step 4: Add the Two Triangle Areas Together
Total Area=Area1+Area2\text{Total Area} = \text{Area}_1 + \text{Area}_2Total Area=Area1+Area2
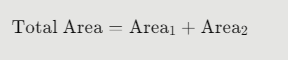
Example: Irregular Quadrilateral Shape
Suppose you have a plot shaped like a quadrilateral with the following sides and diagonal:
- Triangle 1 sides: 6 m, 7 m, 8 m
- Triangle 2 sides: 6 m, 7.5 m, 9 m
Triangle 1:
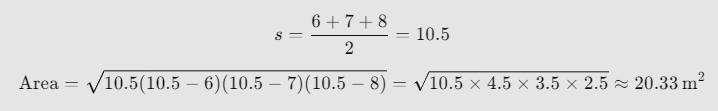
Triangle 2:
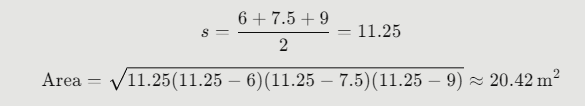
Total Area:
≈20.33+20.42=40.75 m2≈ 20.33 + 20.42 = 40.75 \, \text{m}^2≈20.33+20.42=40.75m2
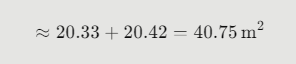
When to Use Heron’s Formula
✅ Use it when:
- The shape has non-right angles
- You know the lengths of all sides
- You can divide the shape into triangles, not perfect rectangles
❌ Avoid it when:
- The shape is already a perfect or nearly perfect rectangle — then use Length × Width
- You don’t have accurate side measurements
Final Thoughts
While Heron’s Formula is typically taught in the context of triangles, its power extends to more complex shapes like irregular rectangles and land plots. By breaking down an irregular shape into triangular parts and applying Heron’s Formula, you can compute areas with surprising accuracy — no need for angles or height measurements.
So next time you’re looking at an oddly-shaped plot or an architectural design, remember: if you know the sides, you know the area — thanks to Heron!